勝利の方程式とは?組み合わせゲーム理論をご紹介!

この記事の目次
はじめに
こんにちは。ITソリューション部(現デジタルテクノロジー戦略本部)のS.Dです。
皆さん、ゲームは好きでしょうか?
私は、将棋やチェスなどのボードゲームが大好きです。
先日、竜王戦の第二局が行われ、タイトル100期を目指す羽生善治先生が、現タイトル保持者の豊島竜王に挑み、1対1のタイになりました。
最近では、将棋AIがプロ棋士よりも強くなり、アマチュア、プロを問わず将棋AIを活用して将棋の研究が行われています。
チェスの世界では、私が生まれるよりも早く、人間が機械に敗れています。カスパロフさんという、当時の世界チャンピオンがDeepBlueと呼ばれるIBMが開発した機械に敗れました。
そして、ついこの間、機械が人間に勝つにはあと10年かかるといわれていた囲碁でも、Google傘下のDeep Mind社の開発したAlpha Goが、現役最強のイ・セドル9段を破ったことで非常に有名になりました。
少し前までは、個人で機械学習やAIなどの開発を行うには、機材などがとても高価で手が出ませんでした。
しかし、AWSやGoogle Cloudなどの、クラウドサービスが台頭してから、個人でも機械学習などの開発が盛んに行えるようになりました。
私も、囲碁の評価関数やAIを趣味で自作しており、いつの間にか自分より強くなってしまいました。
開発を行っている中で、「"ゲーム"とはいったい何なのか?」という問いがよく浮かんできます。
この、組み合わせゲーム理論はゲーム理論の中でも、不偏ゲームという比較的簡単なゲームを対象にした理論です。
とても面白いものなので、皆さんにご紹介できればと思います!
組み合わせゲーム理論とは?
組み合わせゲーム理論(Combinatorial Game Theory)とは、Nim・将棋・チェス・囲碁などの、二人零和有限確定完全情報ゲームに関しての理論です。
ゲームには、勝ち・負け・引き分けの3つの状態があります。(引き分けは存在しないこともあります)
先後が決まっており、状態遷移で勝負が決まります。例えば、将棋では玉が詰まされたら負けです。
手番は、交互に代わり、最終的に手が無くなるとき(=つまり状態遷移がこれ以上進まないとき)に、勝ち負けや、引き分けになります。
組み合わせゲームは、必ず終わりがあり、ループは認められません。
一般的なゲーム理論との大きな違いは、運や不完全情報を含まない点です。
CGT(Combinatorial Game Theory、組み合わせゲーム理論)は、しばしば競プロとかで出問されていて、その多くは、ある発見をすると簡単にコーディングできます。
今回は、その端緒をご紹介します。
不偏ゲーム(Impartial Games)と非不偏ゲーム(Partisan Games)
組み合わせゲームは大きく分けて、不偏ゲーム(Impartial Games)と非不偏ゲーム(Partisan Games)の2つに分けられます。
- 不偏ゲーム:任意の局面において、2人のプレイヤーの選択肢とその結果が同じ
- 非不偏ゲーム:ある局面において、2人のプレイヤーの選択しとその結果が同じでない場合が存在する
例えば、以下のようなゲームは不偏ゲームです。
Nim: 各山にいくつかの石があります。 各ターンで、プレイヤーは1つの山(少なくとも石が1つ存在する)を選び、任意の数の石(少なくとも1つ)を取り除きます。 最初に上の操作ができないプレイヤーが、敗北です。
上記は、非常に有名な不偏ゲームの一つで、Nimと呼ばれています。
逆に、将棋・チェス・囲碁を考えてみましょう。
両ゲームとも、自分の持ち駒(石)と相手の持ち駒(石)があり、両方のプレイヤーにとって選択肢は違い、動かせる駒や石も違います。このようなゲームは、非不偏ゲームと呼ばれます。
非不偏ゲームは、不偏ゲームと比べてはるかに分析が困難になることが多いです。
今回は、不偏ゲームを扱っていきます。
代表的な不偏ゲーム「Nim」について
Nimとは
まずは、Nimゲームについて考察していきましょう。
Nim: 各山にいくつかの石があります。 各ターンで、プレイヤーは1つの山(少なくとも石が1つ存在する)を選び、任意の数の石(少なくとも1つ)を取り除きます。 最初に上の操作ができないプレイヤーが、敗北です。
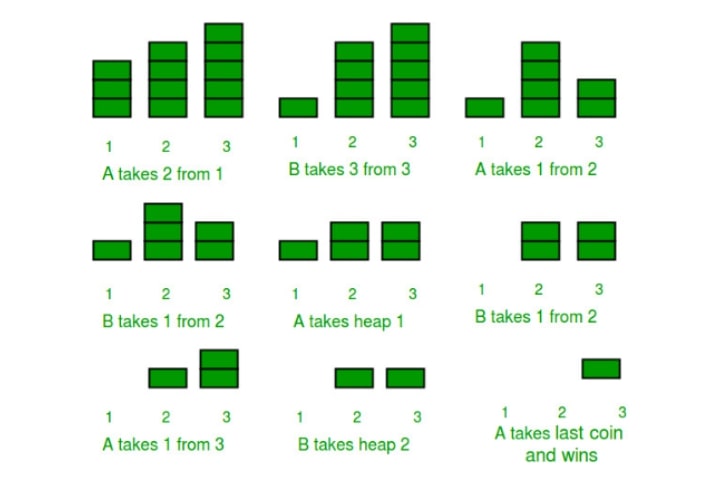
(出典:https://www.geeksforgeeks.org/introduction-to-combinatorial-game-theory/?ref=lbp )
上の例をみていきましょう。
A・Bのプレイヤーがいます。山が3つ存在していて、それぞれ、3・4・5個の石があります。
A->B->A->B->…のような感じで、先手がAとして、任意の山から石を少なくとも1個以上取ります。最終的に、石が取れなくなったプレイヤーの負けです。
上の図のように遷移したとき、Aが勝利します。
さて、このゲームは必勝法が存在するのでしょうか?
また、必勝法が存在するとしたら、先手後手どちらが必ず勝つことができるのでしょうか?
Nimの必勝法とは
Nimには、必勝法が存在します。
ただし、山の石の配置の仕方によって、勝つプレイヤーは変わってきます。
ここで一つ、Nim-Sumと呼ばれる、重要な値を紹介します。
Nim-Sum:ゲームある時点での、各山の石の数の累積XORの値
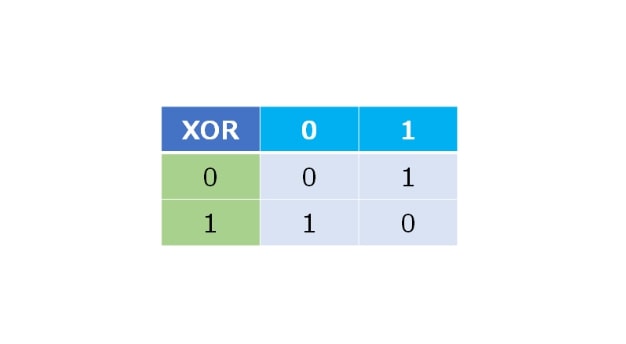
(出典:https://qiita.com/kuuso1/items/778acaa7011d98a3ff3a )
ちなみに、XORとは上のような演算子です。C/C++だと、a ^ b のbit演算子のことです。
このNim-Sumの値を使うと、今回の勝負について以下のことがいえます。
AとBが自分にとって最適な行動(自分が勝つように動く)をとるとき、ゲーム開始時点で、 Nim-Sumが0でなければ、Aの勝ち Nim-Sumが0のとき、Bの勝ち
つまり最適な戦略を考えるには、以下2つの定理が必要です。
定理1. n個の数値のXORの合計が、0のとき数値を一つ減らすだけで、XOR合計を0にすることはできない 定理2. nこの数値のXORの合計が、0以外のとき数値を一つ減らすだけで、XOR合計を0にすることができる
Case1:最初のNim-Sumがゼロの場合
すでに紹介したように、この場合最適に動けば、Bが必ず勝ちます。
Bの最適な戦略として、AのターンのときにNim-Sumを必ずゼロにすることです。
Aの手番のとき、Nim-Sumは、もともとゼロなので、Aがどの山からどれだけ石を取ろうとも、Nim-Sumをゼロにすることはできません。(定理2.)
逆に、Bの手番のとき、Nim-Sumはゼロではないので、必ずNim-Sumをゼロにするような石の取り方が存在します。
ゲームは、最終的に全ての山に石が存在しなくなるまで行われるので、上の手順を繰り返せば、最終的にBが勝つことができます。
この手順、つまり相手のNim-Sumがゼロになるように動くことが、本ゲームでの最適な行動といえます。
Case2:最初のNim-Sumがゼロではない場合
上と同様に、今度は逆にAがBのNim-Sumをゼロにするように動けば必ずAが勝ちます。
Bは常に自分のターンがNim-Sumがゼロで回ってくるので、AのターンにNim-Sumをゼロにすることができません。
例えば、上で例を挙げた、3つの山にそれぞれ、3・4・5個の石が存在する場合は、
3 XOR 4 XOR 5 = 2
となって、必ずAが勝ちます。
Grundy数について
ここからは、Nimを一般化したNimkを扱います。
Nimkは、以下のように表されます。
Nimk: 各山にいくつかの石があります。 各ターンで、プレイヤーは1つの山(少なくとも石が1つ存在する)を選び、K個の石(少なくとも1つ)を取り除きます。 最初に上の操作ができないプレイヤーが、敗北です。
NimkにはGrundy数というものが、密接にかかわっています。
Grundy数とは
Grundy数(Nimbers)とは、ゲームの状態を決定する数字のことです。
全ての不偏ゲームは、一度そのゲームのGrundy数を計算すると、ゲームをどのように解くことができるかがわかります。
※Sprague-Grundyの定理とも呼ばれる
Grundy数を計算する前に、まずMexとは何かを説明します。
Mexとは
Mex(Minimum excludant)とは、ある集合の要素でない最小の非負整数のことです。
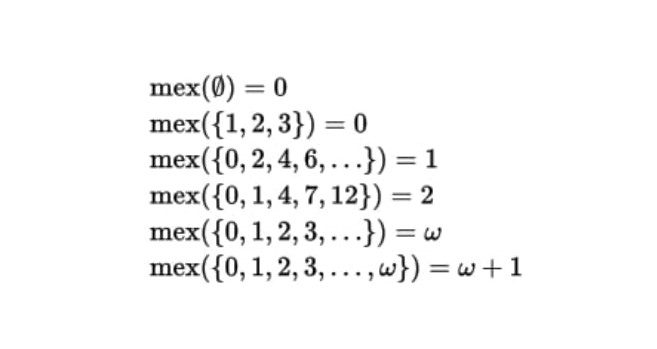
(出展:https://www.geeksforgeeks.org/combinatorial-game-theory-set-3-grundy-numbersnimbers-and-mex/)
Grundy数の計算
今回、Grundy数を以下のように定義します。
Grundy数: 先手のプレイヤーが次の手番で負けることが決定しているときは「0」 それ以外のときは「すべての可能な次の局面のGrundy数のMex」
例で、Grundy数を2つ計算してみましょう!
例1 一つの山に、n個の石があります。 プレイヤーA・Bは、Aを先手として、交互に任意の自然数の数を選んで、山から石を取ります。 最初に、石を取ることができなくなったプレイヤーの敗北です。 A・B共に、自分が勝つために最善な行動をとる場合、どちらが勝利するでしょうか?
上のGrundy数を求めます。
もし山に1つも、石がなかった場合Grundy数G(0) = 0 です。
もし山に1つ石があった場合、Aは必ず石を1つ以上取らなければいけないので、G(1) = Mex(0) = 1
もし山に2つ石があった場合、Aは石を、1つ取るか2つ取るかできます。
G(2) = Mex(0,1) = 2
同様にして、山にn個石があった場合
G(n) = Mex(n-1,n-2,….,1,0) = n
となります。
常にGrundy数が0以上なのでプレイヤーAが必ず勝利します。
例2 1つの山に、n個の石があります。 プレイヤーA・Bは、Aを先手として、交互に1~3までの任意の数を選んで山から石をとります。 最初に、山から石を取ることができなくなったプレイヤーの敗北です。 A・Bともに自分が勝つために最善を尽くした場合、どちらが勝利するでしょうか?
上のGrundy数を求めます。
もし山に1つも、石がなかった場合Grundy数G(0) = 0 です。
もし山に1つ石があった場合、Aは必ず石を1つ以上取らなければいけないので、G(1) = Mex(0) = 1
もし山に2つ石があった場合、Aは石を、1つ取るか2つ取るかできます。
G(2) = Mex(0,1) = 2
もし山に3つ石があった場合、Aは石を、1つ取るか2つ取るか3つ取るかできます。
G(3) = Mex(0,1,2) = 3
ここまでは、例1と同じです。
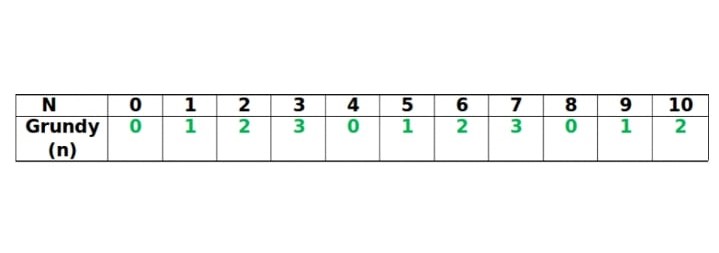
もし山に4つ石があった場合、Aは石を、1つ取るか2つ取るか3つ取るかできます。
G(4) = Mex(1,2,3) = 0
となります!
数学的帰納法から、簡単に
山にn個石があった場合のGrundy数は以下のように求められます。
G(n) = Mex(G(n-1), G(n-2), G(n-3))
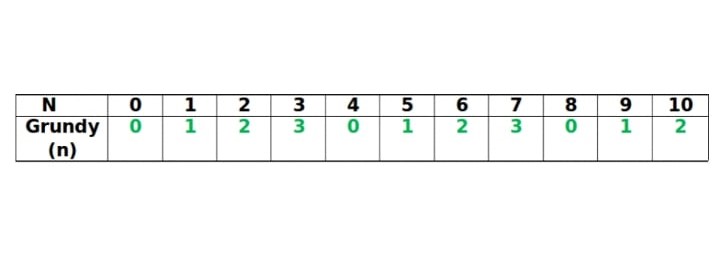
(出典:https://www.geeksforgeeks.org/introduction-to-combinatorial-game-theory/?ref=lbp )
Sprague-Grundy定理について
上の最後の例2について、さらに考察していきましょう。
例2 1つの山に、n個の石があります。 プレイヤーA・Bは、Aを先手として、交互に1~3までの任意の数を選んで山から石をとります。 最初に、山から石を取ることができなくなったプレイヤーの敗北です。 A・Bともに自分が勝つために最善を尽くした場合、どちらが勝利するでしょうか?
この問題は、nが与えられたとき、上のようなGrundy数の遷移で解けることがわかりましたが、一般に不偏ゲームにおいてGrundy数が適用できるのでしょうか?
Sprauge-Grundy定理とは
一般に、2人のプレイヤー(A先手・B後手)がいて、n個のサブゲームからなる不偏ゲームを考えます。
Sprauge-Grundy定理は、以下のことを述べています。
A・Bが、自身の勝利のために最善を尽くして動く場合、 ゲーム開始時に、すべてのサブゲームでのGrundy数のXORが0でない場合は、Aが勝利します。 逆に0のときは、必ずBが勝利します。
定理の適用
Sprauge-Grundy定理は、以下のように適用できます。
- ゲームをサブゲームに分割する
- すべてのサブゲームで、その時点でのGrundy数を計算する
- 計算したGrundy数のXORを計算する
- XORが0でなければ、最初にプレーするプレイヤーが勝ちます。0であれば、後手が勝ちます。
このアルゴリズムで、問題を解くと以下のようになります。
例2 3つの山に、それぞれ、3・4・5個の石があります。 プレイヤーは、Aを先手として、交互に1~3までの任意の数を選んで山から石をとります。 最初に、山から石を取ることができなくなったプレイヤーの敗北です。 A・Bともに自分が勝つために最善を尽くした場合、どちらが勝利するでしょうか?
- 一つの山から石を取りつくすことをサブゲームとします。
- Grundy数を計算します。
(出典:https://www.geeksforgeeks.org/introduction-to-combinatorial-game-theory/?ref=lbp )
- それぞれ3・4・5個の山のGrundy数のXOR
G(3) = 3 G(4) = 0 G(5) = 1 G(3) XOR G(4) XOR G(5) = 2
となります。
4. Grundy数のXORが0ではないので、プレイヤーAが勝利します。
最後に
いかがでしたでしょうか?
楽しんでいただければ幸いです。
CodeForcesやHackerRankなどで、面白い問題がたくさんあるのでぜひ解いてみてください!
全く関係ないですが、とっても楽しいゲームなので、ぜひこれをやってみてください!
Herbert Online Judge : http://herbert.tealang.info/index.php?lang=en
<問題集>
HackerRank
CodeForces
YukiCoder
※本記事は2021年01月時点の情報です。




