Pythonの高速化ライブラリを使ってCos類似度を高速化する

前書きは前提内容になりますので、読み飛ばしてもらって結構です。

前書き

IEEE Spectrumによると、Pythonは過去6年間、プログラミング言語のトップであり続けています。
Pythonは機械学習アプリケーションの構築にも使用されている言語です。
システム職の方はご存知かと思いますが、Pythonはインタプリタ言語です。そのため開発のスピードは上がります。
しかし実行時には毎回コンパイルと各ステートメントの実行が必要なため、実行速度は他の言語との中で比較的遅くなります。これがスケーリング時に問題になることもあります。

このことから、「高速化するためにはほかのコンパイラ型言語のようにPythonのコードを一度コンパイルするか、少なくともその一部をコンパイルすればよいのではないか？」という疑問がわいてきます。

そこで今回はNumbaを使ってPythonの高速化を図りたいと思います。

Numbaとは

Numbaは、PythonとNumpyのコードを一部高速な機械語に変化するオープンソースのJIT(Just In Time)コンパイラです。Numpyの配列や関数と一緒に使うことを想定して設計されています。
配列指向で数学的に重いPythonのコードを最適化してくれます。

本記事の目的

PythonでNumbaを使ってCos類似度計算の高速化を図る！

想定読者

• 日常的にPythonを使用している人
• 高速化ライブラリNumbaを使用したことがない人
• Cos類似度を比較的よく使用する人
• Cos類似度の速度を少しでも速めたい人(重要)

Cos類似度の説明(ご存知の人は飛ばしてください)

Cos類似度とは2つのベクトルが「どのくらい似ているか」という類似性を表す尺度で、具体的には（ベクトル空間における）2つのベクトルがなす角のコサイン値のことです。
この値は2つのベクトルの内積（＝向きと大きさを持つベクトル同士の掛け算）を2つのベクトルの大きさ（＝$ L_2 $ノルム）で割ることで計算されます。

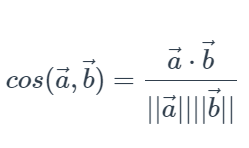
この計算によって値が-1~1の範囲に正規化されるので、Cos類似度が

• 1なら「0度で、同じ向きのベクトル＝完全に似ている」
• 0なら「90度で、独立・直行した向きのベクトル＝似ている・いない、のどちらにも無関係」
• -1なら「180度で、反対向きのベクトル＝完全に似ていない」

という意味になります。
(Cos類似度計算を既存のライブラリで行なう場合、ライブラリによっては逆になることがある。)

参考サイト：コサイン類似度（Cosine Similarity）とは？ - ITmedia

本題

今回はCos類似度計算を高速化したいためPythonのNumbaを使用してどの程度高速化できるのか見てみます。

実験

この実験では、50次元の2つのnumpy配列の間で、Numbaを使用しない場合と使用する場合のコサイン類似度計算を行いました。
まず、Numbaを使用しない場合です。

def cosine_similarity(u:np.ndarray, v:np.ndarray):
    assert(u.shape[0] == v.shape[0])
    uv = 0
    uu = 0
    vv = 0
    for i in range(u.shape[0]):
        uv += u[i]*v[i]
        uu += u[i]*u[i]
        vv += v[i]*v[i]
    cos_theta = 1
    if uu!=0 and vv!=0:
        cos_theta = uv/np.sqrt(uu*vv)
    return cos_theta

次にNumbaを使用した場合です。

from numba import jit

@jit(nopython=True)
def cosine_similarity_numba(u:np.ndarray, v:np.ndarray):
    assert(u.shape[0] == v.shape[0])
    uv = 0
    uu = 0
    vv = 0
    for i in range(u.shape[0]):
        uv += u[i]*v[i]
        uu += u[i]*u[i]
        vv += v[i]*v[i]
    cos_theta = 1
    if uu!=0 and vv!=0:
        cos_theta = uv/np.sqrt(uu*vv)
    return cos_theta

両方の関数を複数の計算回数で実行して、実行時間の違いについてまとめてみました。(実行環境によって多少前後します。)

計算回数	Numbaを使用しない場合	Numbaを使用した場合
1	83.6 μs	1.11 μs
100	8.34 ms	70.9 μs
1,000	86.6 ms	706 μs
10,000	830 ms	7.09 ms
100,000	8.08 s	70.2 ms
1,000,000	1min 27s	699 ms

両対数グラフで示すと以下のようになります。

結果

表にもある通りNumbaを使用した場合のほうが明らかに速いことがわかります。
今回はNumbaを使用してCos類似度計算の高速化を図りましたが、Numbaにはほかにもいろいろと機能があります。
今後もNumbaを使ったPythonの高速化記事を掲載できればと思います。

※本記事は2022年08月時点の内容です。