~マイナビエンジニアからの挑戦状 vol.5~の解説を公開します!

この記事の目次
概要
こんにちは!AIシステム部のS.KとO.Tです。
競プロが趣味の私たちが作成した、オリジナル問題をクリアされた方には、開発エンジニア向けのプログラムに招待させていただく企画を開催しました。
-
2023/04/25
皆さん、こんにちは!毎回大好評の「マイナビエンジニアからの挑戦状」を今回も開催します!ぜひチャレンジしてみてください。
お知らせ
たくさんのご回答ありがとうございました!!
6/16の17:00をもちまして、回答受付は締め切らせていただきました。
本記事では、解説を載せていきたいと思います。
問1:ナンプレ
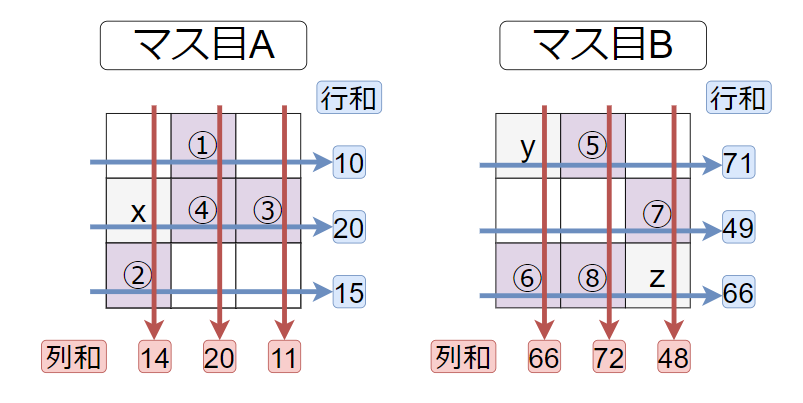
縦横3×3のマス目が2つ用意されている。それぞれマス目Aとマス目Bとする。このマス目に、以下の条件を全て満たすように各マスにa, b, . . . , z の英小文字のアルファベットを一つずつ書き込む。
- 各アルファベットには1, 2, . . . , 26のランダムな番号が割り振られている(下記のテーブルを参照)。
- マス目AとBそれぞれについて、9マスに書き込むアルファベットはそれぞれ異なるものとする。
- マス目AとBそれぞれについて、各行と各列における番号の和は以下の条件を満たしている。
- マス目A
- 1行目, 2行目, 3行目の3マスの番号の和はそれぞれ10, 20 ,15になる。
- 1列目, 2列目, 3列目の3マスの番号の和はそれぞれ14, 20 ,11になる。
- マス目B
- 1行目, 2行目, 3行目の3マスの番号の和はそれぞれ71, 49 ,66になる。
- 1列目, 2列目, 3列目の3マスの番号の和はそれぞれ66, 72 ,48になる。
- マス目A
- マス目AとBそれぞれについて、既に書き込むアルファベットが決まっているマスが存在する。
- マス目A
- 2行1列目に書き込むアルファベットは「x」とする。
- マス目B
- 1行1列目に書き込むアルファベットは「y」とする。
- 3行3列目に書き込むアルファベットは「z」とする。
- マス目A
「①~⑧」のマスに書き込んだアルファベットを、「①②③④ ⑤⑥⑦⑧」の順で並べた英文を答えよ。
| アルファベット | 番号 | アルファベット | 番号 | アルファベット | 番号 |
|---|---|---|---|---|---|
| w | 1 | s | 10 | l | 19 |
| r | 2 | b | 11 | t | 20 |
| o | 3 | p | 12 | a | 21 |
| v | 4 | d | 13 | z | 22 |
| x | 5 | f | 14 | k | 23 |
| c | 6 | j | 15 | m | 24 |
| n | 7 | q | 16 | h | 25 |
| i | 8 | g | 17 | y | 26 |
| e | 9 | u | 18 |
問1の解説
9マスのうち少なくとも4つのマスの値を固定すると、残り5マスの制約を満たすような値が一意に求められる。
この問題ではすでにマス目Aでは1マス、マス目Bでは2マスの値が固定されているため、残りのマスの値について全探索を行い、全ての条件を満たすものを見つけることができる。
今回の条件設定の下では、各マスに入るアルファベットの番号が最大でも17であることが分かるため、$\mathcal{O}(17^3)$で全探索を行うことができる。
以上より、
マス目Aでは、①=n(7), ②=i(8), ③=c(6), ④=e(9)
マス目Bでは、⑤=h(25), ⑥=a(21), ⑦=c(6), ⑧=k(23)
であることがわかる。
答え:「nice hack」
問2:会議室の予約
新人は初めての仕事として、
「〇月×日に行う会議の一覧があるから、全ての会議で使う会議室の予約をしておいて欲しい。」
と上司に頼まれました。
会議室は4つあるので、それぞれの会議で使う会議室を予約する必要があります。
時間が被っている会議を同じ会議室で行うことはできないため、
とは言うものの、条件を満たす様な会議室の使い方はたくさんあるような気がします。
そこで、会議室の予約方法が何通りあるかを答えなさい。
情報
その日行われる会議は10個あり、会議の開始時間と終了時間のリストは以下である。
| 開始時刻 | 終了時刻 |
|---|---|
| 9 | 11 |
| 10 | 12 |
| 17 | 18 |
| 15 | 18 |
| 13 | 15 |
| 11 | 12 |
| 14 | 16 |
| 16 | 17 |
| 15 | 17 |
| 9 | 12 |
会議室の使い方の制約
- 同じ会議室では同時に二つの会議を行うことはできない。
- 会議は時間厳守で行われるため、同じ会議室で11時で終了する会議と、11時から始まる会議を行うことができる。
- 会議室は全部で4つある。
- 全ての会議室を使う必要はない。
問2の解説
各会議で使う可能性がある会議室は4つなので、会議室の使い方は全部で$4^{10}$通り存在している。
この数であれば、全ての場合について会議の時間が被っていないか確かめる全探索を行っても、十分現実的な計算時間(pythonを使っても数秒程度) で処理が終了する。
答え:20736
補足
この問題はグラフ彩色問題と呼ばれる問題に帰着することができる。
これはNP完全問題の一種であることから、会議の数について指数的に計算時間が増加してしまう。
そのため会議の数をこれ以上増やすことは難しいと思われる。
※本記事は2023年06月時点の情報です。





